Heading
The Heading phase represents the developmental stage between FlagLeafAppearance and HeadEmergence in wheat crops. It models the progression of time and environmental responses that lead to the visible emergence of the crop’s head.
Overview
The GenericPhase model simulates the time between the FlagLeafAppearance and HeadEmergence stages.
- The Heading simulates the transition from flag leaf appearance to head emergence.
- The model uses daily Thermal Time, retrieved from the
[Phenology].ThermalTimefunction. - The Target thermal time is depending on photoperiod response and fixed constant of thermal time target at long days \[ \text{Target} = \text{LongPpBase} \times \left( 1 + \text{PpSens} \times \text{PpResponse} \right) \]
Where:
- \(\text{LongPpBase}\) = base thermal time under long day condition, i.e. at 20 hours of daylight with default value of 200.0 °Cd
- \(\text{PpSens}\) = sensitivity to photoperiod, with default value of 2 (unitless multiplier)
- \(\text{PpResponse}\) = interpolated modifier (0 to 1) based on day length
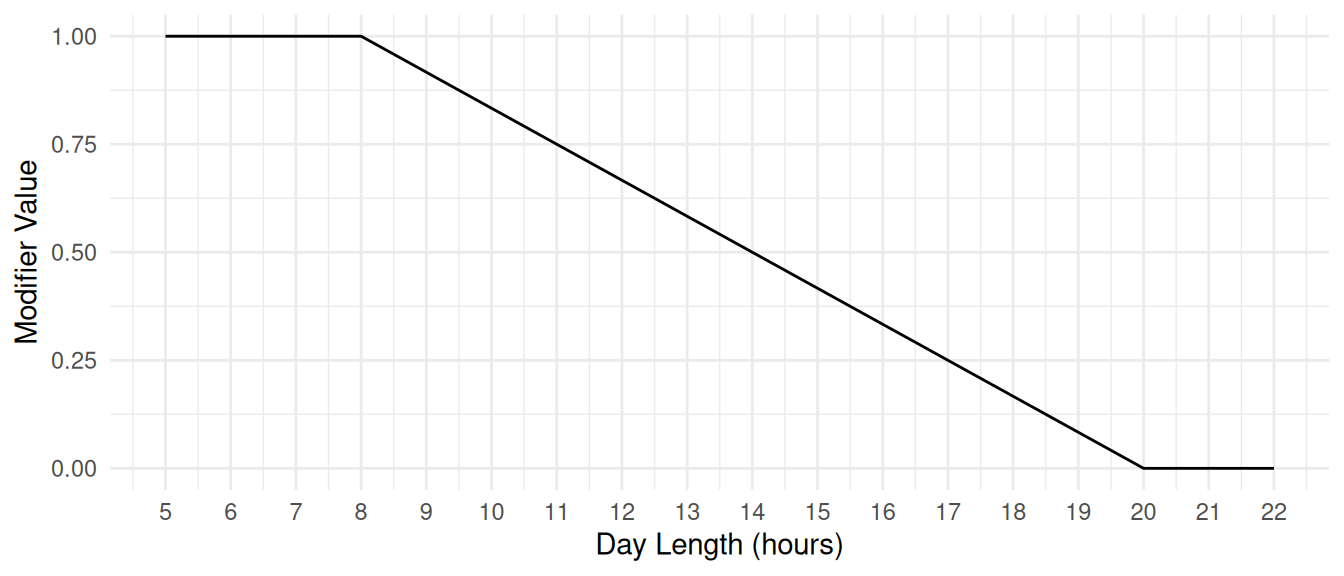
The photoperiod response is modeled using a piecewise linear interpolation:
| Photoperiod (h) | Response |
|---|---|
| 6.0 | 1.0 |
| 8.0 | 1.0 |
| 20.0 | 0.0 |
| 22.0 | 0.0 |
The daily Photoperiod is calculated using the PhotoperiodFunction with 6 degrees twilight.
Cultivar-Specific Parameters
These parameters can vary between crop cultivars and are typically found in the Phenology module:
| Name | Description | Default Value |
|---|---|---|
| [Phenology].HeadEmergenceLongDayBase.FixedValue | Base thermal time (°Cd) required under long days | 200 |
| [Phenology].HeadEmergencePpSensitivity.FixedValue | Sensitivity to photoperiod (unitless multiplier) | 2 |
Practical Example
Effect of Photoperiod Sensitivity on Heading Phase Let’s recalculate the target thermal time for a day length of 12 hours. The photoperiod response \(f_d(12)\) can be interpolated from the table above:
- Between 8 h (response = 1.0) and 20 h (response = 0.0), the response decreases linearly.
- \(f_d(12) = 1.0 - \frac{12 - 8}{20 - 8} = 1.0 - \frac{4}{12} = 1.0 - 0.333 = 0.667\)
Now, for each \(\text{PpSens}\):
| Photoperiod Sensitivity (\(\text{PpSens}\)) | \(1 + \text{PpSens} \times 0.667\) | Target Thermal Time (°C·days) |
|---|---|---|
| 0.0 | \(1 + 0.0 \times 0.667 = 1.000\) | \(200 \times 1.000 = 200.0\) |
| 0.5 | \(1 + 0.5 \times 0.667 = 1.333\) | \(200 \times 1.333 = 266.7\) |
| 1.0 | \(1 + 1.0 \times 0.667 = 1.667\) | \(200 \times 1.667 = 333.3\) |
| 1.5 | \(1 + 1.5 \times 0.667 = 2.000\) | \(200 \times 2.000 = 400.0\) |
| 2.0 | \(1 + 2.0 \times 0.667 = 2.333\) | \(200 \times 2.333 = 466.7\) |